Делители. НОК и НОД.
- Делители. НОК и НОД.
Деление нацело в математике. Отличия от деления нацело в большинстве ЯП.
Как уже было сказано на первой лекции, результат деления в С++ будет зависеть от типов данных, которые вы пытаетесь поделить.
cout << 1 / 2; // 0
cout << double (1) / 2; // 0.5
Поиск всех натуральных делителей числа перебором от 1 до N.
Попробуем решить задачу поиска всех делителей числа. Напоминаем, что число b является делителем числа a,
если a % b == 0
Нам необходимо перебрать все числа от 1 до N. Для каждого из чисел мы будем проверять истинность этого условия.
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
{
if (n % i == 0)
{
cout << i << ' ';
}
}
Пары делителей, обратные делители. Поиск делителей перебором до sqrt(N)
Для делителя b числа a обратным делителем будет являться такое число c, что b * c == a
Заметим, что не существует делителей числа N отличных от самого N, которые были бы больше \(\sqrt{N}\)
При линейном переборе не имеет смысла рассматривать числа большие чем \(\sqrt{N}\).
#include<cmath>
#include<iostream>
using namespace std;
int main()
{
int n, sqrtN;
cin >> n;
sqrtN = sqrt(N);
for (int i = 1; i < sqrtN; ++i)
{
if(n % i == 0)
{
cout << i << ' ' << n / i << '\n';
}
}
if (sqrtN * sqrtN == n)
{
cout << sqrtN;
}
}
Казалось бы, небольшое изменение логики программы ведёт к огромному уменьшению времени работы кода.
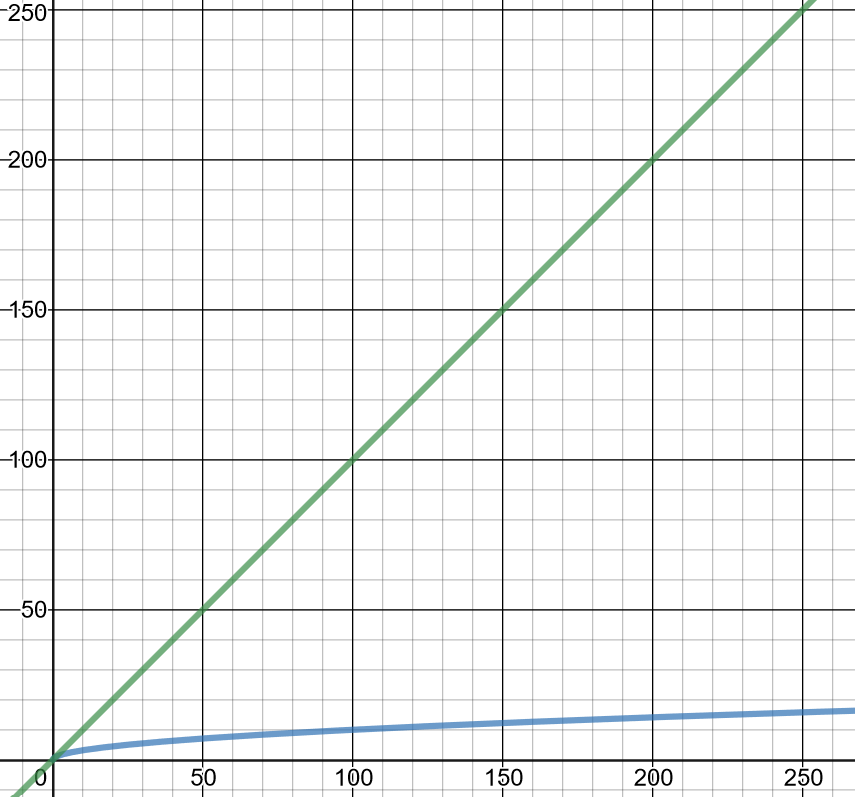
Наибольший общий делитель и наименьшее общее кратное.
Наименьшее общее кратное (НОК) двух целых чисел m и n (не равны нулю) есть наименьшее натуральное число, которое делится на m и n без остатка. Часто записывается как [m,n].
Наибольшим общим делителем (НОД) для двух целых чисел m и n (не равны нулю) называется наибольший из их общих делителей. Часто записывается как (m,n)
| Важно знать, что $$\frac{ | m n | }{(m,n)} = [m,n]$$ |
Алгоритм Евклида.
Алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел. В данном конспекте рассматриваем алгоритмы для натуральных чисел.
С вычитанием.
- Из большего числа вычитаем меньшее.
- Если получается 0, то значит, что числа равны друг другу и являются НОД.
- Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
- Переходим к пункту 1.
Реализацию гуглите сами ГЫ
С делением.
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД.
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Реализацию гуглите сами ГЫ
Для любителей докопаться до истины: https://habr.com/en/post/205106/